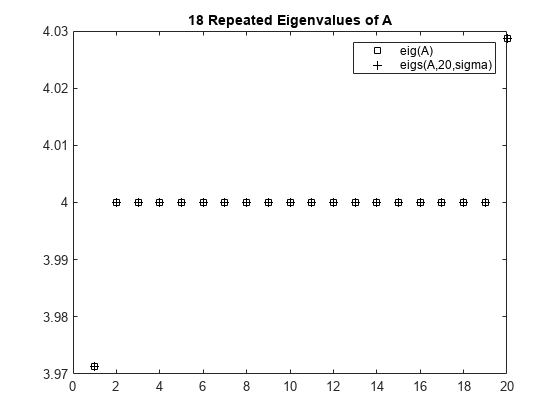
krotstocks.blogg.se - Matlab 2012 left eigenvectors

#Matlab 2012 left eigenvectors full#

These roots are called the eigenvalues of A. The above equation is coined as the characteristic equation of the input matrix ‘M’, and which is a nth order polynomial in λ with n roots.

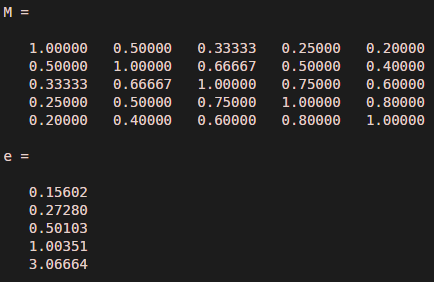
When v is non zero vector then the equation will have a solution only when The eigenvalue equation can also be stated as: The vector corresponding to an Eigenvalue is called an eigenvector. The set of values that can replace for λ and the above equation results a solution, is the set of eigenvalues or characteristic values for the matrix M. Where v is an n-by-1 non-zero vector and λ is a scalar factor.

Case2: multiple outputs, such as = eig(M), then the return form ofeigenvalues is a diagonal matrix, D.Īs we have discussed earlier, eigenvalue(s) for a given input matrix ‘M’ satisfies the equation of :.

Case1: Single output, i.e e = eig(M), then the return form of eigenvalues is a column vector.

The behavior also depends on the number of outputs being specified. The eigenvalue option supports two values as ‘vector’ or ‘matrix’ that decides the form of Eigenvalues is a column vector or a diagonal matrix. Irrespective of the algorithm being specified, eig() function always applies the QZ algorithm where P or Q is not symmetric.ģ. This algorithm also supports solving the eigenvalue problem where matrix ‘P’ is symmetric (Hermitian) and ‘Q’ is symmetric (Hermitian) positive definite.Ģ. If the parameter ‘algorithm’ is excluded from the command, the functioneigchoosesthe algorithm depending on the properties of P and Q.īy default, the selected algorithm is ‘chol’.

It results in the eigenvalues in the form which is specified as eigvalOption.ġ. This algorithm works for non-symmetry matrices as well. ‘qz’:QZ algorithm is used, which is also known as generalised Schur decomposition.‘chol’: the generalized eigenvalues of P and Qare copmutedusing the Cholesky factorization of Q.The parameter ‘algorithm’ decides on how the Eigenvalues will be computed depending on the properties of P and Q. It results in using the balanceOptionparameter is to decide on enabling or disabling of the preliminary balancing step in the algorithm while solving Eigenvalues for the matrix M.

#Matlab 2012 left eigenvectors full#

It results in full matrix M F whose columns are the corresponding left eigenvectors so that M F‘*P = D*M F‘*Q. It results in diagonal matrix M D of generalized eigenvalues and full matrix V whose columns are the corresponding right eigenvectors, so that M*V = Q*V* M D. It results in a column vector that contains the generalized eigenvalues of square matrices P and Q. It results in full matrix M Fwhose columns are the corresponding left eigenvectors, so that M F‘*M = M D* M F‘. It results ina diagonal matrix M D of eigenvalues and matrix V whose columns are the corresponding right eigenvectors, so that M*V = V*M. It results in a column vector consisting of the eigenvalues with respect to the square matrix M. Syntaxīelow awe will understand the syntax with description: Syntax The values of v corresponding to that satisfy the equation are counted as the right eigenvectors. The values corresponding to λ that satisfy the equation specified in the above form, are counted as eigenvalues. Where M is an n-by-n input matrix, ‘v’ is a column vector having a length of size ‘n’, and λ is a scalar factor. Hadoop, Data Science, Statistics & others